Policy Gradients是强化学(Reinforcement Learning)中的一种算法,Policy Gradients 不需要用贪婪策略来选择行为,而是算法直接给出不同行为的概率并通过这个概率来选择行为。
下面是Policy Gradients算法的伪代码: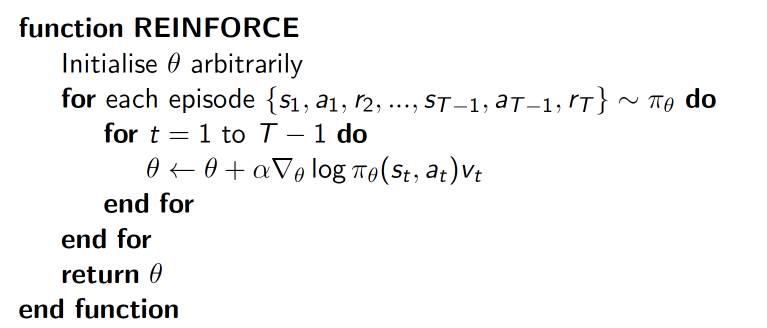
算法中$v_t$是累计回报率(通常需要归一化处理),累计回报越大的状态跟新幅度也越大,这样也可以提高算法的收敛速度。$\pi_\theta(s_t,a_t)$是神经网络根据状态输出的策略。神经网络在输出之前加了一层softmax层,这样可以得到不同行为的概率,行为选择的时候便根据得到的不同行为的概率来选择行为。
Policy Gradients算法在每次迭代之后进行学习,每一次迭代相对独立,因此每一次训练所用的数据也是相对独立的,每一次训练都能利用行为序列中的所有信息。而DQN中需要在运行若干步之后随机采样来进行学习,而跟算法的迭代的次数(算法中的episode)无关,而且DQN中每隔若干步进行学习是样本序列是在存储空间随机采样得到的,这样算法的效率略低,但是DQN所需要的存储空间也会相对较小(可以人为设置)。
Policy Gradients中的$v_t$是累计回报率,跟整个行为序列有关,所以需要在整个行为序列结束之后再进行学习。而DQN中用到的是时间差分的方法,更新时只跟下一次的状态和行为值有关,所以DQN中测存储的状态行为值可以随机采样来进行学习。
Policy Gradients算法中的神将网络直接输出某一状态下不同行为的概率,可以利用得到的概率直接进行行为的选择,这样可以有效地避免算法陷入局部最优。而DQN输出的是不同行为对应的值,因此还需要过$\epsilon$贪婪策略来对行为进行选择。
Policy Gradients需要完整的一组行为序列,得到行为序列之后再反向计算每一个状态的累计回报值,然后才能对神经网络进行训练。DQN则不必等到每一次迭代完成之后才进行训练,而是在给定的若干步之后便可以在存储空间中随机采样并对神经网络进行训练。
Policy的训练依据是累计回报值,回报值跟当前迭代的整个行为序列有关,回报值越高则说明行为越正确。DQN的修正依据是每一步的奖励值,只跟当前状态和下一状态有关,奖励值越高则说明行为越正确。
因此,虽然Policy Gradients 和 DQN 都是在强化学习算法中采用了神将网络的方法对行为值进行近似计算,但本质的思想是不一样的。 Policy Gradients 采用的蒙特卡洛方法来计算行为值(累计回报)。在DQN中则是用到时间差分的方法(TD方法)来计算行为值。
参考资料:

