本文主要介绍Python在数据处理中用到的库和方法。
这篇文章本质上是一篇翻译文,原文是Python Numpy Tutorial。
Python是一门优秀的通用编程语言,再结合一些流行的库(numpy,scipy,matplotlib)它会成为强大的科学计算环境。
Python
python是一门高级的动态类型的多模式编程语言。Python代码经常被说成是伪代码,因为它可以让你用可读性很强的几行代码来实现一些有力的想法。下面是一个用Python实现的经典的快速排序算法。
1 2 3 4 5 6 7 8 9 10 11
| def quicksort(arr): if len(arr) <= 1: return arr pivot = arr[len(arr) // 2] left = [x for x in arr if x < pivot] middle = [x for x in arr if x == pivot] right = [x for x in arr if x > pivot] return quicksort(left) + middle + quicksort(right) print(quicksort([3,6,8,10,1,2,1]))
|
Python版本
目前,Python有两个不同的受支持版本2.7和3.5。令人困惑的是Python3.0引入了许多向后不兼容的改变,因此2.7版本下的代码在3.5中不一定有效,反之亦然。本教程的代码使用的是Python3.5。
可以通过命令行运行Python --version来检查你的Python版本。
基本数据类型
像大多数编程语言一样,Python有许多基本的数据类型,包括整型、浮点型、布尔型和字符串。这些数据类型的操作方式和其他编程语言类似。
数字:整型和浮点型的工作方式和其他编程语言类似:
1 2 3 4 5 6 7 8 9 10 11 12 13 14
| x = 3 print(type(x)) print(x) print(x + 1) print(x - 1) print(x * 2) print(x ** 2) x += 1 print(x) x *= 2 print(x) y = 2.5 print(type(y)) print(y, y + 1, y * 2, y ** 2)
|
注意:与其他编程语言不同,Python没有自加(x++)和自减(x--)操作。
Python也有内建的复数类型,具体内容可以参考官方文档
布尔值:Python可以通过英文单词来实现常用的布尔逻辑操作,而不是使用符号(&&,||,等):
1 2 3 4 5 6 7
| t = True f = False print(type(t)) print(t and f) print(t or f) print(not t) print(t != f)
|
字符串:Python可以很好地支持字符串操作:
1 2 3 4 5 6 7 8
| hello = 'hello' world = "world" print(hello) print(len(hello)) hw = hello + ' ' + world print(hw) hw12 = '%s %s %d' % (hello, world, 12) print(hw12)
|
字符串对象有许多非常有用的方法,比如:
1 2 3 4 5 6 7 8
| s = "hello" print(s.capitalize()) print(s.upper()) print(s.rjust(7)) print(s.center(7)) print(s.replace('l', '(ell)')) print(' world '.strip())
|
你可以通过官方文档来查找所有的字符串方法。
容器
Python包含几个内建的容器类型:列表、字典、集合和元组。
列表
Python中列表等效于数组,并且可以调整大小以及包含其他类型的元素:
1 2 3 4 5 6 7 8 9
| xs = [3, 1, 2] print(xs, xs[2]) print(xs[-1]) xs[2] = 'foo' print(xs) xs.append('bar') print(xs) x = xs.pop() print(x, xs)
|
你也可以在官方文档中查找列表的详细资料。
切片:除了每次可以获取列表中的元素之外,Python还提供了简明的语法来获取子列表。这就是所谓的切片:
1 2 3 4 5 6 7 8 9
| nums = list(range(5)) print(nums) print(nums[2:4]) print(nums[2:]) print(nums[:2]) print(nums[:]) print(nums[:-1]) nums[2:4] = [8, 9] print(nums)
|
我们还将会在numpy的数部分作中遇到切片操作。
循环:你可以像下面的例子一样通过列表中的元素来实现循环:
1 2 3 4
| animals = ['cat', 'dog', 'monkey'] for animal in animals: print(animal)
|
如果想要得到每一个元素在循环体中的索引,可以使用内建函数enumerate():
1 2 3 4
| animals = ['cat', 'dog', 'monkey'] for idx, animal in enumerate(animals): print('#%d: %s' % (idx + 1, animal))
|
列表解析:在编程过程中,通常我们会将一种类型的数据转换为其他类型,考虑下面计算平方数的例子:
1 2 3 4 5
| nums = [0, 1, 2, 3, 4] squares = [] for x in nums: squares.append(x ** 2) print(squares)
|
你可以利用简单地利用列表解析来实现:
1 2 3
| nums = [0, 1, 2, 3, 4] squares = [x ** 2 for x in nums] print(squares)
|
列表解析可以包含条件:
1 2 3
| nums = [0, 1, 2, 3, 4] even_squares = [x ** 2 for x in nums if x % 2 == 0] print(even_squares)
|
字典
字典存储键值对(关键词,数值),类似于Java中的Map和JavaScript中的对象。可以通过下面的例子来使用字典:
1 2 3 4 5 6 7 8 9 10
| d = {'cat': 'cute', 'dog': 'furry'} print(d['cat']) print('cat' in d) d['fish'] = 'wet' print(d['fish']) print(d.get('monkey', 'N/A')) print(d.get('fish', 'N/A')) del d['fish'] print(d.get('fish', 'N/A'))
|
可以在官方文档中查找需要的有关字典的信息。
循环:可以简单地通过字典中的关键字来进行迭代:
1 2 3 4 5
| d = {'person': 2, 'cat': 4, 'spider': 8} for animal in d: legs = d[animal] print('A %s has %d legs' % (animal, legs))
|
如果想要得到字典中的关键字和相对应的数值,可以使用items方法来实现:
1 2 3 4
| d = {'person': 2, 'cat': 4, 'spider': 8} for animal, legs in d.items(): print('A %s has %d legs' % (animal, legs))
|
字典解析:与列表解析类似,可以方便地构造字典。例如:
1 2 3
| nums = [0, 1, 2, 3, 4] even_num_to_square = {x: x ** 2 for x in nums if x % 2 == 0} print(even_num_to_square)
|
集合
集合是不同元素的无序集合。思考下面的例子:
1 2 3 4 5 6 7 8 9 10
| animals = {'cat', 'dog'} print('cat' in animals) print('fish' in animals) animals.add('fish') print('fish' in animals) print(len(animals)) animals.add('cat') print(len(animals)) animals.remove('cat') print(len(animals))
|
同样可以在官方文档中查找更详细的信息。
循环:通过集合迭代和通过列表迭代有相同的语法。但是由于集合是无序的,因此不能假设所访问的集合中元素的顺序:
1 2 3 4
| animals = {'cat', 'dog', 'fish'} for idx, animal in enumerate(animals): print('#%d: %s' % (idx + 1, animal))
|
集合解析:与列表解析和字典解析类似,我们可以使用集合解析快速地构造集合:
1 2 3
| from math import sqrt nums = {int(sqrt(x)) for x in range(30)} print(nums)
|
元组
元组是(不可改变的)有序的值列表,元组在许多方面和列表类似,最重要的一点不同是元组可以作为字典中的关键字和集合中的元素,而列表不行。下面是一些小例子:
1 2 3 4 5
| d = {(x, x + 1): x for x in range(10)} t = (5, 6) print(type(t)) print(d[t]) print(d[(1, 2)])
|
关于元组的官方文档
函数
Python中的函数通过关键字def来定义。例如:
1 2 3 4 5 6 7 8 9 10 11
| def sign(x): if x > 0: return 'positive' elif x < 0: return 'negative' else: return 'zero' for x in [-1, 0, 1]: print(sign(x))
|
通常会采用可选关键字参数来定义函数,例如:
1 2 3 4 5 6 7 8
| def hello(name, loud=False): if loud: print('HELLO, %s!' % name.upper()) else: print('Hello, %s' % name) hello('Bob') hello('Fred', loud=True)
|
有关Python函数的更多信息可以参考官方文档
类
Python中定义类的语法非常简洁:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
| class Greeter(object): def __init__(self, name): self.name = name def greet(self, loud=False): if loud: print('HELLO, %s!' % self.name.upper()) else: print('Hello, %s' % self.name) g = Greeter('Fred') g.greet() g.greet(loud=True)
|
Python中类的官方文档
Numpy
Numpy是Python科学计算的核心库。它提供可高性能的多维数组对象以及处理多维数组的工具。如果你已经熟悉MATLAB,你会发现教程对你入门Numpy非常有用。
数组
Numpy中的数组是类型相同,由非负整数构成的元组索引的值的网格。维数是数组的秩(rank),矩阵的形状(shape)是一个整数元组,表示每一个维度的大小。
可以通过嵌套Python列表的方式来初始化numpy数组,可以通过方括号来获取数组中的元素:
1 2 3 4 5 6 7 8 9 10 11 12
| import numpy as np a = np.array([1, 2, 3]) print(type(a)) print(a.shape) print(a[0], a[1], a[2]) a[0] = 5 print(a) b = np.array([[1,2,3],[4,5,6]]) print(b.shape) print(b[0, 0], b[0, 1], b[1, 0])
|
Numpy也提供了很多函数用来创建数组:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
| import numpy as np a = np.zeros((2,2)) print(a) b = np.ones((1,2)) print(b) c = np.full((2,2), 7) print(c) d = np.eye(2) print(d) e = np.random.random((2,2)) print(e)
|
可以通过官方文档来查找更多数组创建的方法。
数组索引
Numpy提供了几种数组索引的方法。
切片:类似于Python中的列表,numpy中的数组也可以切片。由于数组有时候是多维的,所以一定要明确数组中每一维度上的切片:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
| import numpy as np a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]]) b = a[:2, 1:3] print(a[0, 1]) b[0, 0] = 77 print(a[0, 1])
|
可以混合使用整数索引和切片索引。然而,这样做需要数组的秩要低于原始数组。注意,这和MATLAB中数组切片的操作不同:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
| import numpy as np a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]]) row_r1 = a[1, :] row_r2 = a[1:2, :] print(row_r1, row_r1.shape) print(row_r2, row_r2.shape) col_r1 = a[:, 1] col_r2 = a[:, 1:2] print(col_r1, col_r1.shape) print(col_r2, col_r2.shape)
|
整数数组索引:当使用切片来索引numpy的数组时,结果被视为是原始阵列的一个子阵列。相反,整数数组索引可以利用其它数组中的数据来构造任意的数组。例如:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
| import numpy as np a = np.array([[1,2], [3, 4], [5, 6]]) print(a[[0, 1, 2], [0, 1, 0]]) print(np.array([a[0, 0], a[1, 1], a[2, 0]])) print(a[[0, 0], [1, 1]]) print(np.array([a[0, 1], a[0, 1]]))
|
整数数组索引的一个有用的技巧是用用来选择或改变矩阵中每一列的元素
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
| import numpy as np a = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]]) print(a) b = np.array([0, 2, 0, 1]) print(a[np.arange(4), b]) a[np.arange(4), b] += 10 print(a)
|
布尔数组索引:布尔数组索引可以挑出数组中的任意元素。通常这用索引用来选择数组中满足一定条件的数组。例如:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
| import numpy as np a = np.array([[1,2], [3, 4], [5, 6]]) bool_idx = (a > 2) print(bool_idx) print(a[bool_idx]) print(a[a > 2])
|
想要了解更多关于numpy数组索引的信息,可以阅读官方文档
数据类型
每一个numpy数组是一个有相同类型元素的网格。Numpy提供了许多用来构造数组的数据类型。当你在创建数组的时候Numpy会尝试猜测数组的类型,但是构造数组通常包括一个可选参数来明确数组的数据类型。例如:
1 2 3 4 5 6 7 8 9 10
| import numpy as np x = np.array([1, 2]) print(x.dtype) x = np.array([1.0, 2.0]) print(x.dtype) x = np.array([1, 2], dtype=np.int64) print(x.dtype)
|
更多关于numpy的数据类型请参考官方文档
数据计算
在Numpy模块中基本的针对数组元素的数学公式操作可以通过运算符重载或函数来实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
| import numpy as np x = np.array([[1,2],[3,4]], dtype=np.float64) y = np.array([[5,6],[7,8]], dtype=np.float64) print(x + y) print(np.add(x, y)) print(x - y) print(np.subtract(x, y)) print(x * y) print(np.multiply(x, y)) print(x / y) print(np.divide(x, y)) print(np.sqrt(x))
|
注意,不像在MATLAB中,*是元素间相乘,而不是矩阵相乘。我们使用dot函数来计算向量的内积,来实现矩阵乘法。dot可以通过模块函数或者数组对象的方法来实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
| import numpy as np x = np.array([[1,2],[3,4]]) y = np.array([[5,6],[7,8]]) v = np.array([9,10]) w = np.array([11, 12]) print(v.dot(w)) print(np.dot(v, w)) print(x.dot(v)) print(np.dot(x, v)) print(x.dot(y)) print(np.dot(x, y))
|
Numpy在矩阵运算中提供了许多有用的函数,最常用的函数之一是sum:
1 2 3 4 5 6 7
| import numpy as np x = np.array([[1,2],[3,4]]) print(np.sum(x)) print(np.sum(x, axis=0)) print(np.sum(x, axis=1))
|
可以在官方文档中查看完整的数学函数列表。
除了使用数组来计算数学函数之外,通常需要改变数组形状或者其他队数组中数据的操作,最简单的例子是矩阵的转置操作;通过数组对象的T转置可以简单地实现矩阵的转置。
1 2 3 4 5 6 7 8 9 10 11 12
| import numpy as np x = np.array([[1,2], [3,4]]) print(x) print(x.T) v = np.array([1,2,3]) print(v) print(v.T)
|
Numpy提供了许多函数来对数组进行操作,完整的函数列表请参考官方文档
广播
广播是一种非常强大的机制,可以允许numpy中不同形状的数组执行算术运算。通常情况下当有一个小数组和一个大数组时,想要用小数组在大数组上多次执行某些操作。
比如,想给矩阵的每一行加上常数向量。方法如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
| import numpy as np x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]]) v = np.array([1, 0, 1]) y = np.empty_like(x) for i in range(4): y[i, :] = x[i, :] + v print(y)
|
然而当矩阵x非常大的时候,Python中计算循环会变得很慢。注意到在矩阵x的每一行加上向量v等效于通过垂直复制v来构造矩阵vv,然后对x和vv执行元素间求和。实现方法如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
| import numpy as np x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]]) v = np.array([1, 0, 1]) vv = np.tile(v, (4, 1)) print(vv) y = x + vv print(y)
|
Numpy广播允许执行这样的操作而不必创造多重复制的v,使用广播来实现:
1 2 3 4 5 6 7 8 9 10 11
| import numpy as np x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]]) v = np.array([1,0,1]) y = x + v print(y)
|
即使x的形状是(4,3)而且v的形状是(3,),但现行方程y = x + v由于广播机制同样有效。这个线性方程仿佛v的形状实际上是(4,3),其中每一行都是v的复制,然后在执行元素间求和。
两个矩阵执行广播需要遵循以下规则:
- 如果数组具有不同的秩,用1来填充秩较低的数组的形状,直到数组具有相同的长度。
- 数组在这一维度中被称为兼容的,如果两个数组在某一维度中的大小的是相同的,或者其中一个数组的在某一维度中的大小是1。
- 如果数组在所有维度上都是兼容的,则数组可以执行广播操作合并在一起。
- 广播操作之后,数组的形状等于两个输入数组形状元素的最大值。
- 在任何维度中,如果一个数组的形状为1并且另一个数组的形状大于1,第一个数组沿这个维度进行复制操作。
如果以上解释不明白的话,请参考官方文档的解释或者其他解释
支持广播功能被称作通用功能,可以在官方文档中查看所有通用功能。
下面是一些广播功能的应用:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42
| import numpy as np v = np.array([1,2,3]) w = np.array([4,5]) print(np.reshape(v, (3, 1)) * w) x = np.array([[1,2,3], [4,5,6]]) print(x + v) print((x.T + w).T) print(x + np.reshape(w, (2, 1))) print(x * 2)
|
广播功能可以使代码更加简洁和高效,因此可以尽可能地使用这用方法。
以上是Numpy中重要内容的简明概述,但实际远不止如此。可以在numpy参考中查看更多关于numpy的资料。
SciPy
Numpy提供了高性能的多维数组的基本计算和操作工具,Scipy在这基础上,提供了大量用来操作numpy数组的函数,在不同的科学和工程领域都十分有用。
最有效的了解SciPy的方法是阅读官方文档,这里会重点介绍SciPy中常用的部分。
图像操作
SciPy提供可一些图像操作的基本功能。例如,将磁盘中的图片读取到numpy数组中,将数组中的图像写入到磁盘中,以及改变图片的大小。下面是一些用来展示以上功能的小例子:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
| from scipy.misc import imread, imsave, imresize img = imread('assets/cat.jpg') print(img.dtype, img.shape) img_tinted = img * [1, 0.95, 0.9] img_tinted = imresize(img_tinted, (300, 300)) imsave('assets/cat_tinted.jpg', img_tinted)
|
原始图片
修改颜色和大小之后的图片
Matlab文件
函数scipy.io.loadmat和scipy.io.savemat可以对MATLAB文件进行读写,详细说明请参考官方文档
两点间距离
Scipy定义了许多函数用来计算集合中坐标点之间的距离
函数scipy.spatial.distance.pdist可以计算集合中所有点之间的距离:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
| import numpy as np from scipy.spatial.distance import pdist, squareform x = np.array([[0, 1], [1, 0], [2, 0]]) print(x) d = squareform(pdist(x, 'euclidean')) print(d)
|
关于这个函数的详细资料可以阅读官方文档
Matplotlib
Matplotlib是一个绘图库,本节内容将简明介绍matplotlib.pyplot模块,该模块提供了与MATLAB类似的绘图系统。
类似的函数(scipy.spatial.distance.cdist)计算两个集合之间点的距离。官方文档
绘图
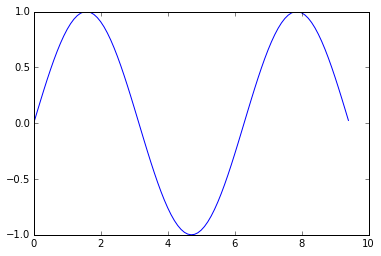
matplotlib中最重要的函数是plot,该函数可以绘制2D数据,例如“
1 2 3 4 5 6 7 8 9 10
| import numpy as np import matplotlib.pyplot as plt x = np.arange(0, 3 * np.pi, 0.1) y = np.sin(x) plt.plot(x, y) plt.show()
|
运行上面的代码可以得到下面的图:
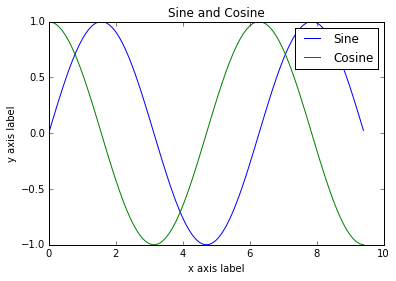
仅仅需要少量的额外工作就可以简单地绘制多条曲线,并且添加标题,图例和坐标轴
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
| import numpy as np import matplotlib.pyplot as plt x = np.arange(0, 3 * np.pi, 0.1) y_sin = np.sin(x) y_cos = np.cos(x) plt.plot(x, y_sin) plt.plot(x, y_cos) plt.xlabel('x axis label') plt.ylabel('y axis label') plt.title('Sine and Cosine') plt.legend(['Sine', 'Cosine']) plt.show()
|
可以在官方文档中阅读关于plot的更多资料。
子图
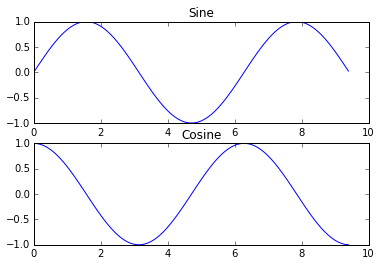
使用subplot函数可以在一张图片上显示不同事物。例子如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
| import numpy as np import matplotlib.pyplot as plt x = np.arange(0, 3 * np.pi, 0.1) y_sin = np.sin(x) y_cos = np.cos(x) plt.subplot(2, 1, 1) plt.plot(x, y_sin) plt.title('Sine') plt.subplot(2, 1, 2) plt.plot(x, y_cos) plt.title('Cosine') plt.show()
|
有关subplot的更多信息请参考官方文档
图像
可以使用imshow函数来显示图像,例如:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
| import numpy as np from scipy.misc import imread, imresize import matplotlib.pyplot as plt img = imread('assets/cat.jpg') img_tinted = img * [1, 0.95, 0.9] plt.subplot(1, 2, 1) plt.imshow(img) plt.subplot(1, 2, 2) plt.imshow(np.uint8(img_tinted)) plt.show()
|