今天介绍强化学习中的一种新的算法,叫做Actor Critic。
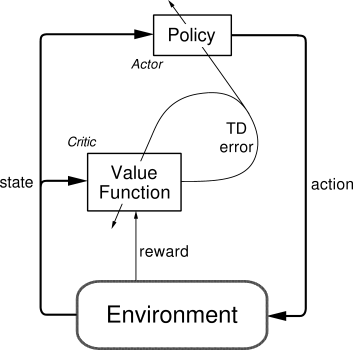
介绍 Actor Critic将Policy Gradient(Actor部分)和Function Approximation(Critic部分)相结合,Actor根据当前状态对应行为的概率选择行为,Critic通过当前状态,奖励值以及下一个状态进行学习同时返回Actor当前行为评分,Actor根据Critic给出的评分对行为概率进行修正。
Actor Critic的优缺点:
优点 :Actor Critic不用想DQN或者Policy Gradient那样需要对探索的状态,动作和奖励信息进行存储。而是可以进行单步学习和更新,这样学习效率要比DQN和Policy Gradient快。缺点 :由于单步更新参照的信息有限,而且Actor和Critic要同时学习,因此学习比较难以收敛。
代码实现 下面介绍Actor Critic的具体实现过程。
试验环境依然使用gym中的CartPole-v0。
首先介绍Actor部分的代码。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Actor (object) :
def __init__ (self, sess, n_features, n_actions, lr=0.001 ) :
self.sess = sess
self.s = tf.placeholder(tf.float32, [1 , n_features], "state" )
self.a = tf.placeholder(tf.int32, None , "act" )
self.td_error = tf.placeholder(tf.float32, None , "td_error" )
with tf.variable_scope('Actor' ):
l1 = tf.layers.dense(
inputs=self.s,
units=20 ,
activation=tf.nn.relu,
kernel_initializer=tf.random_normal_initializer(0. , .1 ),
bias_initializer=tf.constant_initializer(0.1 ),
name='l1'
)
self.acts_prob = tf.layers.dense(
inputs=l1,
units=n_actions,
activation=tf.nn.softmax,
kernel_initializer=tf.random_normal_initializer(0. , .1 ),
bias_initializer=tf.constant_initializer(0.1 ),
name='acts_prob'
)
with tf.variable_scope('exp_v' ):
log_prob = tf.log(self.acts_prob[0 , self.a])
self.exp_v = tf.reduce_mean(log_prob * self.td_error)
with tf.variable_scope('train' ):
self.train_op = tf.train.AdamOptimizer(lr).minimize(-self.exp_v)
def learn (self, s, a, td) :
s = s[np.newaxis, :]
feed_dict = {self.s: s, self.a: a, self.td_error: td}
_, exp_v = self.sess.run([self.train_op, self.exp_v], feed_dict)
return exp_v
def choose_action (self, s) :
s = s[np.newaxis, :]
probs = self.sess.run(self.acts_prob, {self.s: s})
return np.random.choice(np.arange(probs.shape[1 ]), p=probs.ravel())
代码中首先传递环境的状态数量n_features,动作数量n_actions和学习效率lr。然后构建用于Actor学习的神经网络,网络包含一个含有20个节点的隐藏层。Actor.learn()通过当前状态s,动作a和Critic给出的时间差分误差td进行学习。Actor.Choose_action()通过当前状态s计算出每个动作的概率,然后根据相应的概率来选择动作。
下面是Critic部分的代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Critic (object) :
def __init__ (self, sess, n_features, lr=0.01 ) :
self.sess = sess
self.s = tf.placeholder(tf.float32, [1 , n_features], "state" )
self.v_ = tf.placeholder(tf.float32, [1 , 1 ], "v_next" )
self.r = tf.placeholder(tf.float32, None , 'r' )
with tf.variable_scope('Critic' ):
l1 = tf.layers.dense(
inputs=self.s,
units=20 ,
activation=tf.nn.relu,
kernel_initializer=tf.random_normal_initializer(0. , .1 ),
bias_initializer=tf.constant_initializer(0.1 ),
name='l1'
)
self.v = tf.layers.dense(
inputs=l1,
units=1 ,
activation=None ,
kernel_initializer=tf.random_normal_initializer(0. , .1 ),
bias_initializer=tf.constant_initializer(0.1 ),
name='V'
)
with tf.variable_scope('squared_TD_error' ):
self.td_error = self.r + GAMMA * self.v_ - self.v
self.loss = tf.square(self.td_error)
with tf.variable_scope('train' ):
self.train_op = tf.train.AdamOptimizer(lr).minimize(self.loss)
def learn (self, s, r, s_) :
s, s_ = s[np.newaxis, :], s_[np.newaxis, :]
v_ = self.sess.run(self.v, {self.s: s_})
td_error, _ = self.sess.run([self.td_error, self.train_op],
{self.s: s, self.v_: v_, self.r: r})
return td_error
代码中建立一个输入层节点为s,隐藏层节点为20,输出层节点为1的神经网络。Critic.learn()根据当前状态s,奖励值r和下一步的状态s_进行学习,并返回时间差分误差td给actor.learn()
然后是完整的训练过程:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
import gym
from ActorCritic import *
np.random.seed(2 )
tf.set_random_seed(2 )
OUTPUT_GRAPH = False
MAX_EPISODE = 3000
DISPLAY_REWARD_THRESHOLD = 100
MAX_EP_STEPS = 1000
RENDER = False
GAMMA = 0.9
LR_A = 0.001
LR_C = 0.01
env = gym.make('CartPole-v0' )
env.seed(1 )
N_F = env.observation_space.shape[0 ]
N_A = env.action_space.n
sess = tf.Session()
actor = Actor(sess, n_features=N_F, n_actions=N_A, lr=LR_A)
critic = Critic(sess, n_features=N_F, lr=LR_C)
sess.run(tf.global_variables_initializer())
if OUTPUT_GRAPH:
tf.summary.FileWriter("logs/" , sess.graph)
for i_episode in range(MAX_EPISODE):
s = env.reset()
t = 0
track_r = []
while True :
if RENDER: env.render()
a = actor.choose_action(s)
s_, r, done, info = env.step(a)
if done: r = -20
track_r.append(r)
td_error = critic.learn(s, r, s_)
actor.learn(s, a, td_error)
s = s_
t += 1
if done or t >= MAX_EP_STEPS:
ep_rs_sum = sum(track_r)
if 'running_reward' not in globals():
running_reward = ep_rs_sum
else :
running_reward = running_reward * 0.95 + ep_rs_sum * 0.05
if running_reward > DISPLAY_REWARD_THRESHOLD: RENDER = True
print("episode:" , i_episode, " reward:" , int(running_reward))
break
通过训练发下,通过3000次迭代,Actor Critic算法的收敛性确实不是太理想,没有DQN和Policy Gradient的效果好。
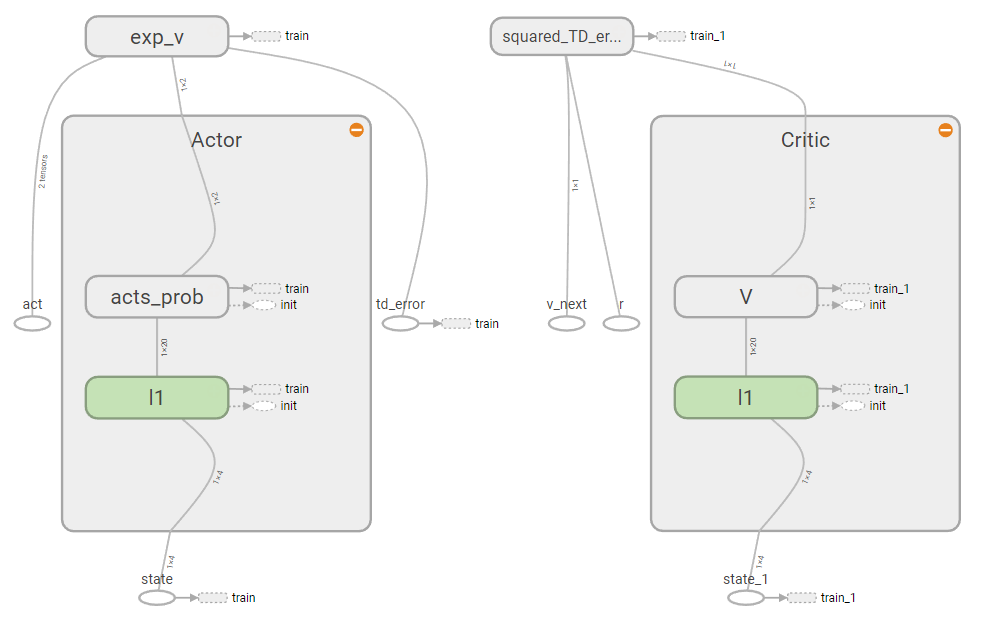
通过TensorBoard可以查看网络的结构如下:1
Tensorboard --logdir logs
参考资料: